Stochastic Process Module

This module contains two different implementation for generating stochastic processes for a given auto correlation function (Karhunen-Loève expansion and Fast-Fourier method). Both methods are based on a time discrete process, however cubic spline interpolation is assured to be valid within a given tolerance.

• Stochastic Process Generators
  • Karhunen-Loève expansion
    • StocProc_KLE
  • Fast-Fourier method
    • StocProc_FFT
• Example

Example

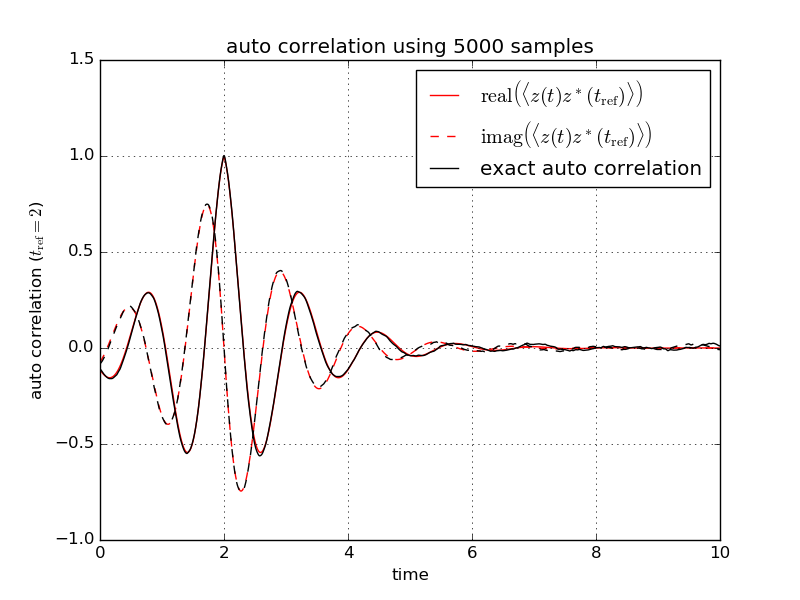
The example will setup a process generator for an exponential auto correlation function and sample a single realization.

def lsd(w):
    # Lorenzian spectral density
    return 1/(1 + (w - _WC_)**2)

def lac(t):
    # the corresponding Lorenzian correlation function
    # note there is a factor of one over pi in the
    # deficition of the correlation function:
    # lac(t) = 1/pi int_{-infty}^infty d w  lsd(w) exp(-i w t)
    return np.exp(- np.abs(t) - 1j*_WC_*t)

t_max = 10
print("setup process generator")
stp = sp.StocProc_FFT_tol(lsd, t_max, lac,
                          negative_frequencies=True, seed=0,
                          intgr_tol=1e-2, intpl_tol=1e-2)
print("generate single process")
stp.new_process()
zt = stp()    # get discrete process

The full example can be found here.

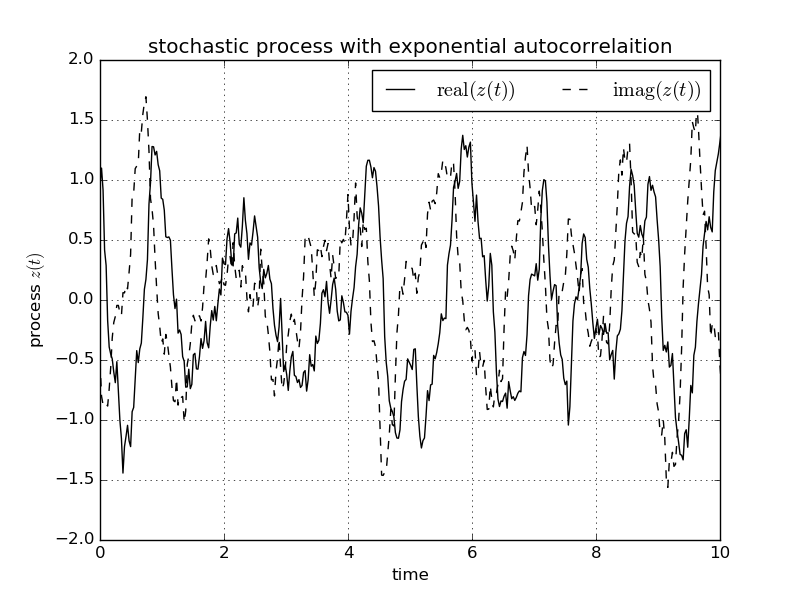
Averaging over 5000 samples yields the auto correlation function which is in good agreement with the exact auto correlation.